Een Finite State Machine voor de H7b flight control
|
In dit artikel zal een toelichting worden gegeven op het ontwerp en de implementatie van een Finite State Machine voor vluchtbesturing. Hoewel deze techniek binnen de softwareontwikkeling wel wordt toegepast, is het gebruik bij de NERO nieuw. Het bleek dan ook dat specifieke aanvullingen nodig waren om deze techniek goed bruikbaar te maken. Ook was het noodzakelijk om een ontwerpmethode voor vluchtbesturingsscenario's te ontwikkelen. Het gebruik van een FSM biedt in veel gevallen voordelen ten opzicht van andere technieken. Deze voordelen liggen met name in de eenvoudige programmering, de hoge betrouwbaarheid en de hoge voorspelbaarheid. Een mogelijk nadeel is het feit dat de achterliggende principes niet eenvoudig te begrijpen zijn. Naar mening van de auteur valt dit nadeel weg tegen de voordelen |
1. het veilig besturen van: separatie, ontsteking van de tweede trap en parachutering;
2. het veilig laten landen van de H7B combinatie;
3. het besturen van het onder 1 genoemde op basis van vaste tijdsinstellingen;
4. het besturen van het onder 1 genoemde op basis van dynamische sensor-informatie;
5. een worst-time gedrag dat gelijk is aan het gebruik van vaste timers.
De ontwerpeisen voor de vluchtbesturingseenheid (Flight Controller) van de H7B zijn de
volgende:
1. hoge voorspelbaarheid, het gedrag van de Flight Controller moet volledig voorspelbaar zijn;
2. hoge betrouwbaarheid, het vluchtbesturingsscenario moet betrouwbaar worden geďmplementeerd;
3. lage stroomconsumptie, de boordbatterij moet niet te zwaar worden belast;
4. geringe omvang, gemeten in elektronicacomponenten.
Het bovenstaande stelt verregaande eisen aan de zowel de gehanteerde ontwerpmethode als de gebruikte implementatiewijze. Zoals zal blijken draagt de FSM bij aan de bij NERO Haarlem aanwezige tendens componenten zo betrouwbaar mogelijk, en niet complexer dan strikt noodzakelijk, te maken.
80,0Kb
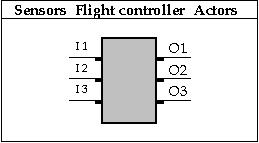
Figuur 1 - De eenvoudige FSM
Een FSM bestaat uit hardware en software. Kenmerkend voor de software bij een FSM is dat alle beslissingsregels in een tweedimensionale tabel (matrix) vastliggen. De software bestaat daarmee in essentie uit een met waarden gevulde matrix. Voor de hardware zijn verschillende implementatievormen denkbaar. Om de werking van een FSM toe te lichten, zal allereerst de basistechniek van de FSM worden toegelicht. Om deze basistechniek voor vluchtbesturing toepasbaar te maken, zijn er vier uitbreidingen nodig. Deze uitbreidingen betreffen achtereenvolgens: 1. de koppeling van output-waarden, waarmee de relatie met de actoren tot stand wordt gebracht; 2. de input-codering, die een relatie met de sensoren legt; 3. het inbrengen van de tijdsafhankelijkheid, waarmee timer-functies mogelijk worden; 4. en tenslotte de mogelijkheid tot een input-fixatie. Zij zullen apart worden toegelicht. Tegelijkertijd zal worden aangegeven hoe een FSM op de hardware kan worden afgebeeld. Begonnen zal worden met een vereenvoudigd voorbeeld, later zal worden ingegaan op de oplossing die voor de H7B is gekozen. De basis FSM Zoals gesteld bestaat een FSM uit een matrix met rijen en kolommen. Een dergelijk matrix met vier kolommen en vijf rijen is geschetst in figuur 2 en wordt een State Transition Table genoemd. Daarbij is een pointer aanwezig die een van de rijen aanwijst: het nummer van de aangewezen rij wordt de toestand (in het Engels: state) genoemd.
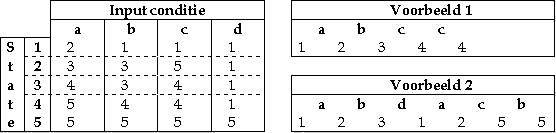
Figuur 2 - Basis FSM
De Input-condities worden in dit voorbeeld beperkt tot vier mogelijkheden, de condities a tot en met d. Het aantal toestanden (states) is in dit voorbeeld beperkt tot vijf. Aan deze beperking ontleent de FSM (eindige toestand machine) tevens zijn naam. Dit geeft een matrix met vijf toestanden en vier input-condities. Wanneer deze matrix (fsm[1..5, a..d] OF 1..5) wordt gevuld met waarden, kan het volgende programma (in pseudo code) worden doorlopen.

Figuur 3 - Het imaginaire algoritme van de basis FSM
Wanneer de input achtereenvolgens de condities a, b, c en c aanneemt, zullen achtereenvolgens de waarden 1, 2, 3, 4, 4 worden afgedrukt (voorbeeld 1). Een input van a, b, b, a, c, b geeft achtereenvolgens de waarden 1, 2, 3, 1, 2, 5, 5 (voorbeeld 2). Op deze wijze is het mogelijk door een combinatie van de toestand met de input-conditie, naar alle cellen in de matrix toe te gaan. Doordat de toestand vastgehouden wordt, is informatie beschikbaar over de historie van de input. Bijvoorbeeld wanneer de toestand vijf is, moet worden verondersteld dat input a in het verleden aangeboden is geweest.
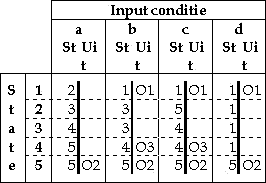
Figuur 4 - Basis FSM met output-signalen
Bij de output-signalen kan een onderscheid worden gemaakt tussen statusinformatie en stuurinformatie (actors). Het hebben van statusinformatie kan noodzakelijk zijn om de toestand waarin de FSM zich bevindt, aan te geven. Een voorbeeld is bijvoorbeeld de Safe/Arm constructie waarmee de Pyro op scherp wordt gesteld. Essentiele statusinformatie is dan een statussignaal wat aangeeft of de FSM zich in de Safe- of Arm-conditie bevind.
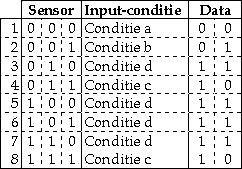
Figuur 5 - Verband tussen sensoren en Input-condities
Hiervoor zal ook de hardware moeten worden uitgebreid. Namelijk met een encoder die de sensorsignalen vertaald in de vier input-condities. Voor deze vier input-condities worden twee datakanalen gebruikt. In de laatste kolom van figuur 5 is aangegeven hoe een input-conditie met behulp van twee datakanalen (BCD-code) kan worden gecodeerd.
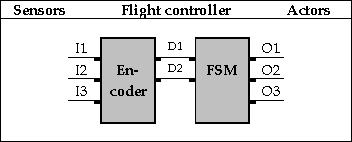
Figuur 6 - De FSM met input-codering

Figuur 7 - Het imaginaire algoritme van de tijdafhankelijke FSM
De FSM wacht hierbij niet meer op nieuwe input (asynchrone FSM), maar neemt in het geval dat geen nieuwe input aanwezig is de laatst aangeboden sensorinformatie als input (synchrone FSM). Daarna wordt steeds een halve seconde gewacht, voordat opnieuw naar de input wordt gekeken. Wanneer de tabel van figuur 4 wordt gecombineerd met dit algoritme, zal wanneer a als input-conditie wordt aangeboden de FSM in twee seconden toestand 5 aannemen. Door de waarden steeds met ‚‚n te verhogen (zoals in kolom is a gedaan) zal de FSM sequentieel de kolom doorlopen. Hierbij worden steeds tijdsstappen genomen van 0,5 seconde.
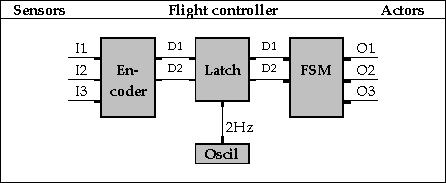
Figuur 8 - De FSM met input-codering en tijdsafhankelijkheid
Ook hiervoor is een hardware-aanpassing noodzakelijk. Tussen de FSM en de encoder wordt een latch geplaatst. Deze latch geeft de ingangssignalen pas door wanneer de oscillator daarvoor een signaal geeft. Het nieuwe schema staat getekend in figuur 8.
Om dit te bewerkstelligen wordt een terugkoppeling aangebracht tussen een van de uitgangssignalen en de oscillator. Wanneer deze uitgang hoog wordt, wordt de oscillator van de latch afgekoppeld en blijft de laatste input van kracht. Hiermee wordt afgedwongen dat de FSM altijd in dezelfde kolom blijft. Dit schema is gegeven in figuur 9.
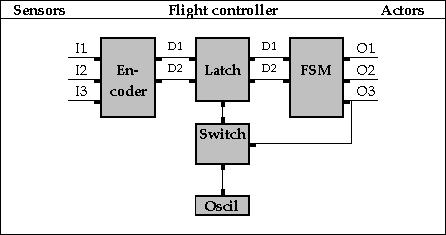
Figuur 9 - De FSM met input-codering, tijdsafhankelijkheid en input-fixatie
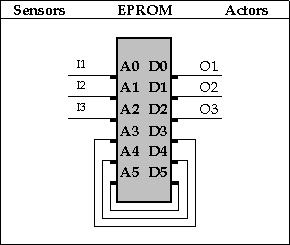
De acht kolommen worden gevormd door de drie input-kanalen, afgebeeld op drie adreslijnen van de EPROM. De overige drie adreslijnen worden gebruikt voor de terugkoppeling en vormen daarmee de acht rijen van de Finitee State Table. Omdat de EPROM in dit voorbeeld per adres zes databits kan vasthouden blijven er tenslotte drie output-kanalen beschikbaar. In figuur 12 is een schema voor een EPROM implementatie gegeven. Daarnaast zijn een aantal andere implementaties mogelijk, die in dit artikel niet verder zullen worden toegelicht. Te denken valt hierbij aan implementaties met behulp van een:
- poortschakeling
- icroprocessor/microcontroller;
- PGA - Field Programmable Gate Array;
- PLD - Erasable Programmable Logic Device;
- chip waarin een programmeerbare FSM is ge‹mplementeerd
Zowel bij de poortschakeling als de FPGA wordt de State Transition Table eenmalig ingebracht. Bij een poortschakeling door een directe vertaling in hardware. Bij een FPGA, wordt de State Transition Table eenmalig ingebrand. De overige oplossingen maken gebruik van geheugen waarin de State Transition Table in een of andere vorm is opgenomen en kan worden aangepast.
Figuur 10 - De implementatie van de FSM
| Signaal | Soort | Betekenis | |
| 1 | ARM | Sensor | De Arm-plug is geplaatst |
| 2 | LO | Sensor | De Lift-off is met breekdraad gedetecteerd. |
| 3 | SEP | Sensor | De separatie is met breekdraad gedetecteerd. |
| 4 | BST | Sensor | De motor ontsteking van de 2e trap is met branddraad gedetecteerd |
| 5 | RST | Input | Reset de FSM naar de beginconditie |
| 6 | Scen1 | Input | Selecteer een van de vier vluchtscenario's |
| 7 | Scen2 | Input | Selecteer een van de vier vluchtscenario's |
| 1 | InFix | Status | De input moet worden gefixeerd |
| 2 | Error | Status | De FSM bevindt zich in een toestand, veroorzaakt door falende sensors |
| 3 | Safe | Status | De FSM bevindt zich in de Safe-toestand |
| 4 | Count | Status | De FSM is aan het tellen, de timers lopen |
| 5 | Separ | Actor | Het signaal voor separatie wordt gegeven |
| 6 | Boost | Actor | Het signaal voor ontsteking 2e trap wordt gegeven |
| 7 | Hatch | Actor | Het signaal voor het uitwerpen van het luik wordt gegeven |
| 8 | Para | Actor | Het signaal voor het loslaten van de hoofdparachute wordt gegeven. |
Figuur 11 - De input- en output-kanalen van de H7b
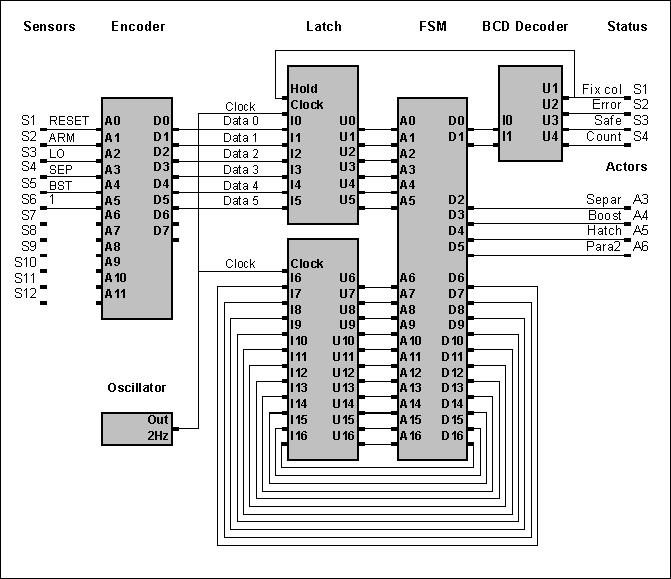
Figuur 12 - EPROM-implementatie van de FSM